平衡二叉树详解
详细介绍下平衡二叉树插入新节点之后,导致了平衡二叉树失衡时,平衡二叉树的自平衡操作流程。以及平衡二叉树删除节点之后,平衡二叉树的自平衡操作流程。
1. 二叉树
本文主要是介绍平衡二叉树,但是因为涉及到了一些基础的二叉树概念,所以简单介绍下
二叉树的所有节点的左子树节点都小于这个节点,其右子树节点都大于这个节点。
二叉树的深度: 深度是任意一个节点到二叉树根节点的距离。(网上存在很多不同的概念,各类文章也是看的人云里雾里,索性按自己想法来,本文里所有地方的根结点深度都算1。)
二叉树的高度: 高度是二叉树中任意一个节点到叶子节点的距离。
计算案例如下
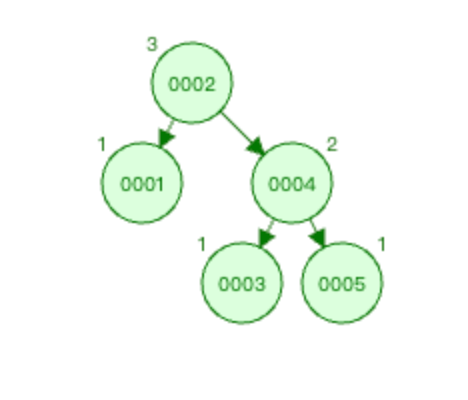
| 节点 | 高度计算路径 | 高度 | 深度计算路径 | 深度 |
|---|---|---|---|---|
| 0002 | 0002-->0004-->0005 | 3 | 0002 | 1 |
| 0001 | 0001 | 1 | 0001-->0002 | 2 |
| 0004 | 0004-->0005 | 2 | 0004-->0002 | 2 |
| 0003 | 0003 | 1 | 0003-->0004-->0002 | 3 |
| 0005 | 0005 | 1 | 0005-->0004-->0002 | 3 |
2. 平衡二叉树的概念
平衡二叉树的根结点是由构建树的整个过程来决定的,一组同样的数据,插入的顺序不一样,得到的根节点和结果树可能是不一样。
平衡二叉树是一个自平衡的二叉查找树,他维护树的高度是平衡的,对于树中的任意节点,其左右子树的高度差或深度差都不超过1。
这里就引入了一个概念,叫 平衡因子 ,即一个根节点的左子树深度减去它右子树深度,得到的结果就是这个根节点的 平衡引子。
示例一
- 叶子节点1、3、5的平衡因子为0。
- 节点2的平衡因子为-1(节点2的左子树深度为2,右子树深度为3)。
- 节点4的平衡因子为0(节点4的左子树深度为2,右子树深度为2)。

平衡二叉树的 平衡因子 的 绝对值 不能大于1,所以上图就是一个标准的平衡二叉树。
示例二
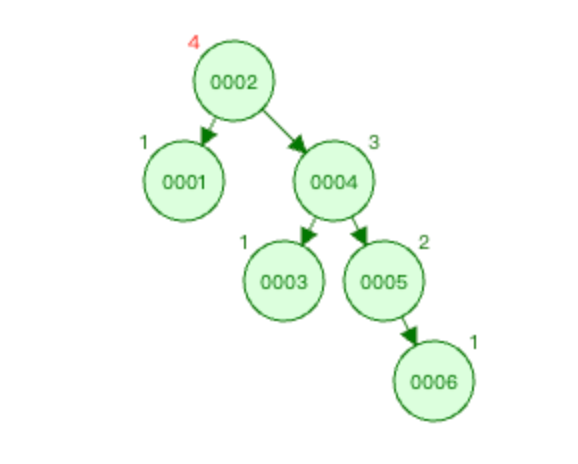
- 叶子节点1、3、6的平衡因子为0。
- 节点2的平衡因子为-2(节点2的左子树深度为2,右子树深度为4)。
- 节点4的平衡因子为-1(节点4的左子树深度为2,右子树深度为3)。
- 节点5的平衡因子为-1(节点4的左子树深度为1,右子树深度为2)。
节点2的 平衡因子 的绝对值大于1,所以上图算不上平衡二叉树。
3. 平衡二叉树的节点插入
插入新节点前是标准平衡二叉树,插入之后,导致其不再是平衡二叉树怎么办呢?
如下图所示,插入前为左,插入后为右。
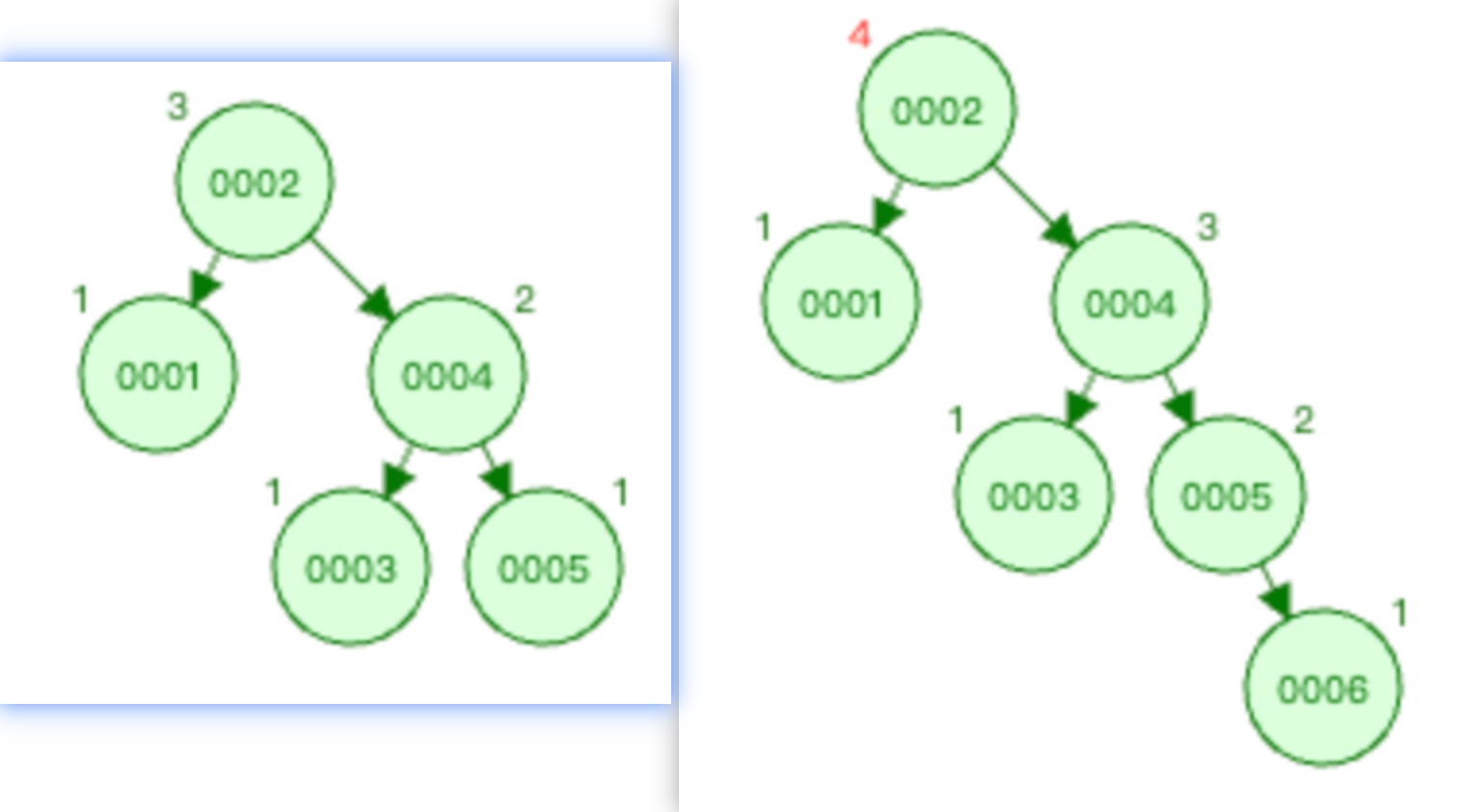
上图所示,在原平衡二叉树的基础上插入一个节点0006,就会破坏这个树的平衡性,根据上文所述的 平衡因子 概念可知,上右图里节点0006的加入,破坏了0002节点的平衡性。这种会破坏树平衡性的节点叫 麻烦节点 ,被破坏平衡性的节点叫做 被破坏节点 (如果有多个节点的平衡性都被破坏了,也只会称距离插入节点最近的被破坏节点为 被破坏节点 )。
破坏平衡性的场景有如下几种,LL型、RR型、LR型、RL型,其中L代表左,R代表右。
从 被破坏节点 开始往下判断两次(两个节点之间的路径为一次判断,路径向左即为L,路径向右即为R)即得到破坏平衡性的场景类型。
3.1 LL型
3.1.1 示例图
图1:
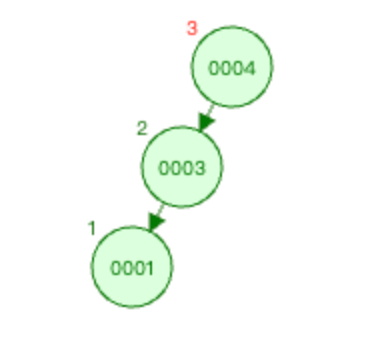
上图1中 麻烦节点 为0001,被破坏节点 为0004。
在 被破坏节点 0004节点的 左边 (0004-->0003为左)节点(0003节点)的 左边 (0003-->0001为左)插入新节点0001。
图2:
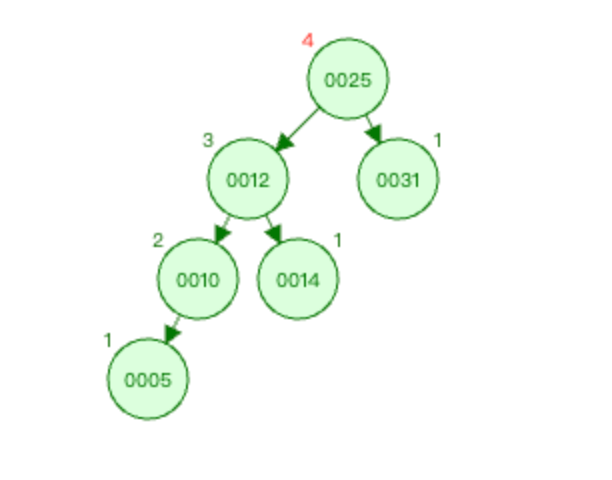
上图2中 麻烦节点 为0005,被破坏节点 为0025。
在 被破坏节点 0025节点的 左边 (0025-->0012为左)节点(0012节点)的 左边 (0012-->0010为左)插入新节点0005。
图3:
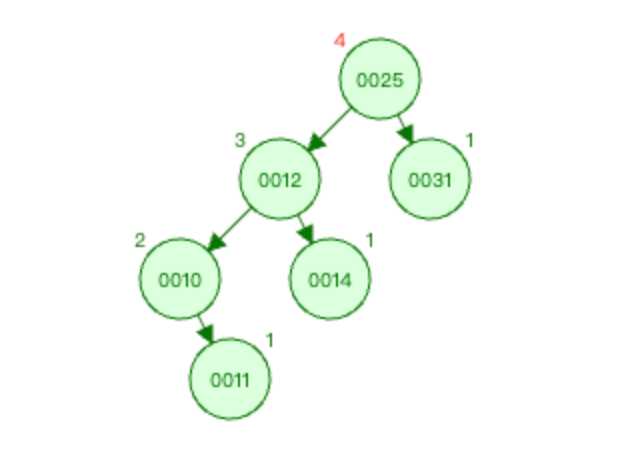
上图3中 麻烦节点 为0011,被破坏节点 为0025。
在 被破坏节点 0025节点的 左边 (0025-->0012为左)节点(0012节点)的 左边 (0012-->0010为左)插入新节点0011。
上面三张图所示,在被破坏节点的左边的左边插入新节点,从而导致平衡树失衡了,则称之为LL型。虽然上面图2的0005节点是在0010节点的左边插入,而图3的0011节点是在0010节点的右边插入,但是它们还都算是LL型。因为上文也说过,只会从 被破坏节点 开始往下判断两次(第一次为0025-->0012,第二次为0012-->0010),不会理会第三次是往左还是往右。
LL型的解决方案是右旋。
3.1.2 什么是右旋?
在网上看的一个很形象的动态示意图,如下
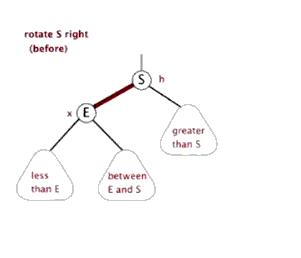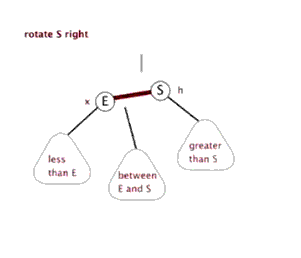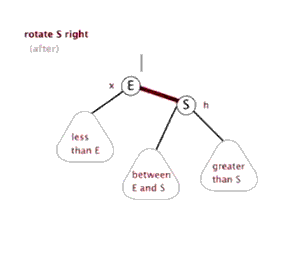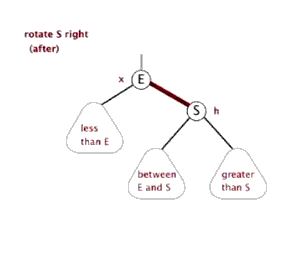
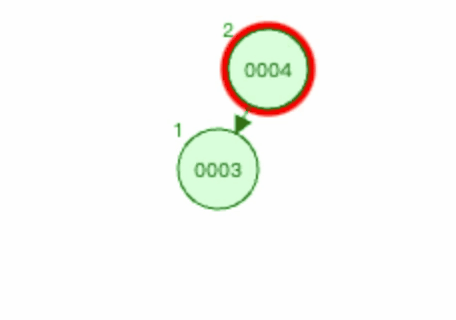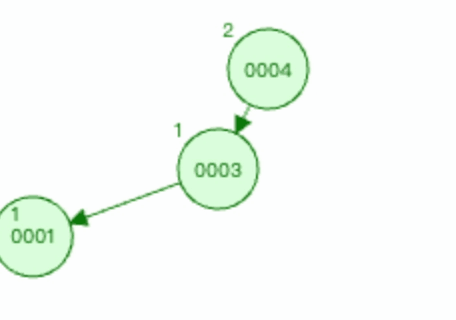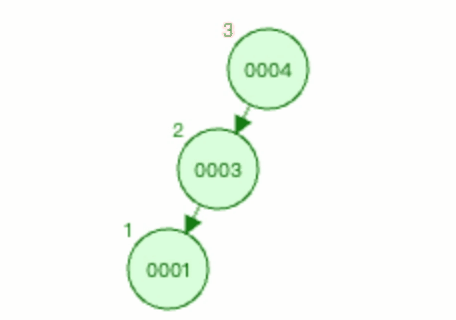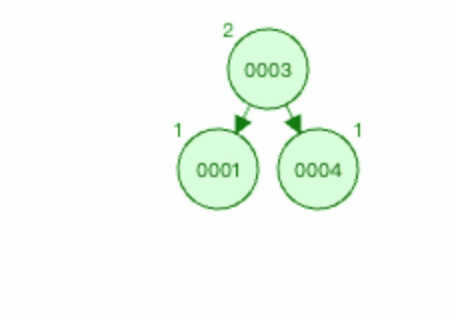
3.1.3 上图1右旋过程如下
以节点0003为基础进行右旋。
3.1.4 上图2右旋过程如下
以节点0012为基础进行右旋。
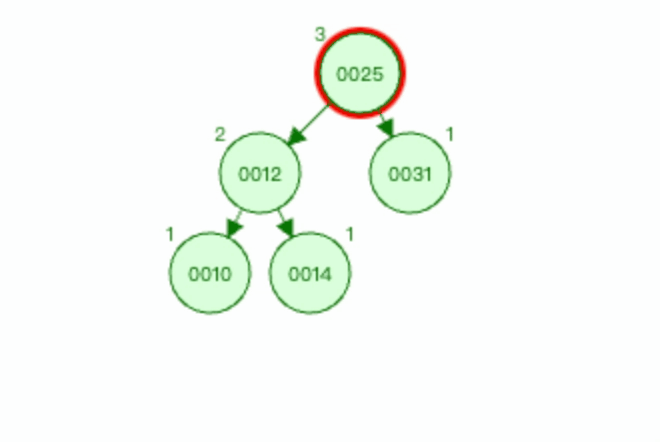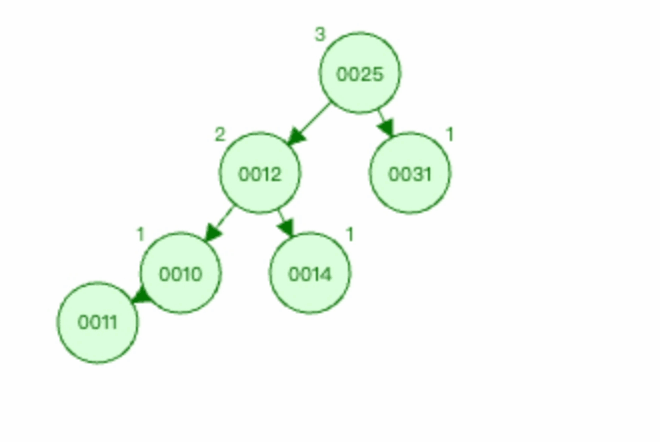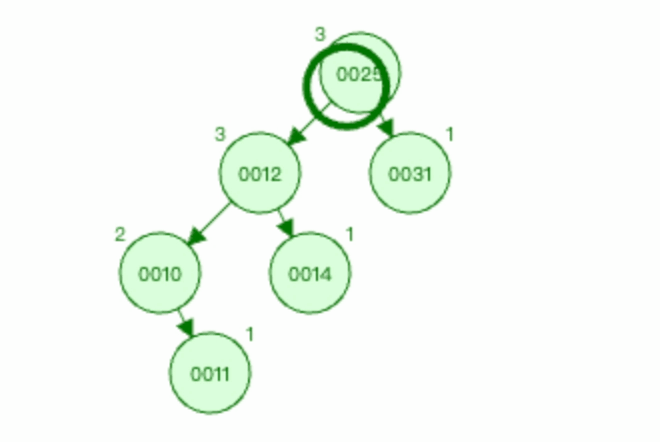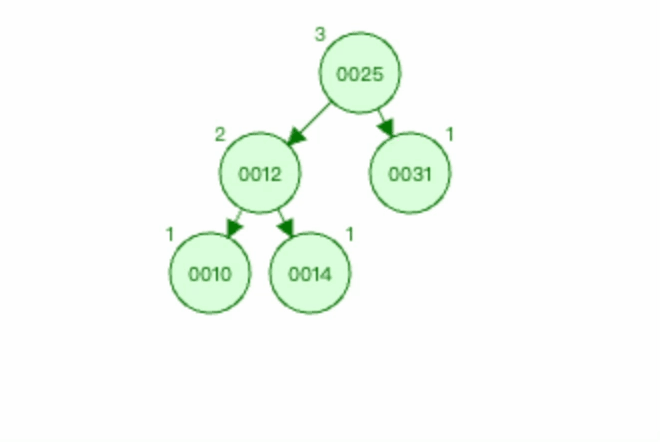
3.1.5 上图3右旋过程如下
以节点0012为基础进行右旋。
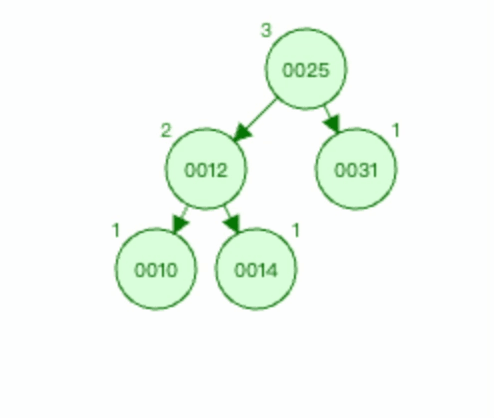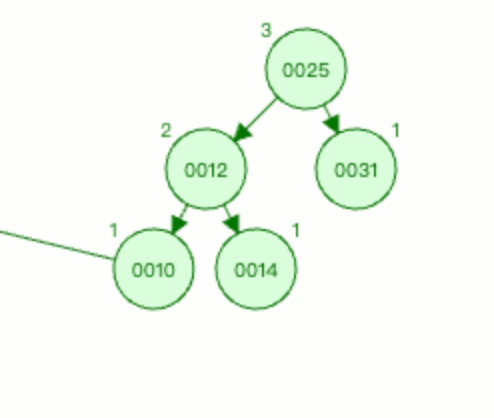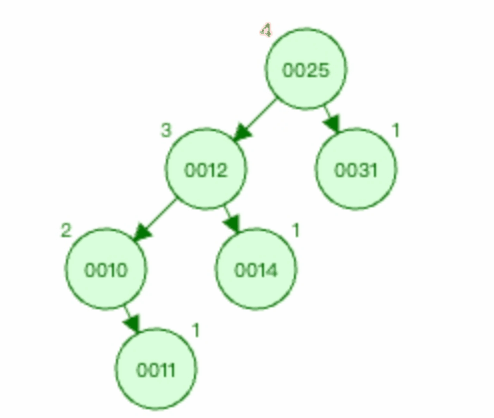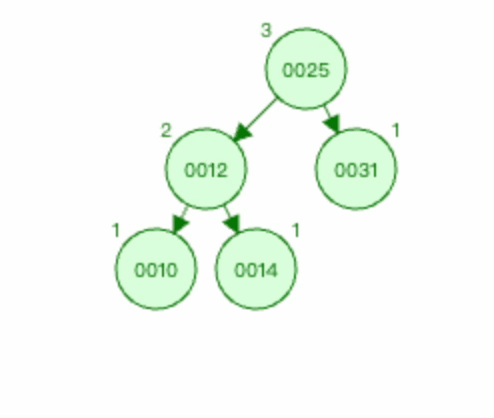
3.2 RR型
3.2.1 示例图
图1:
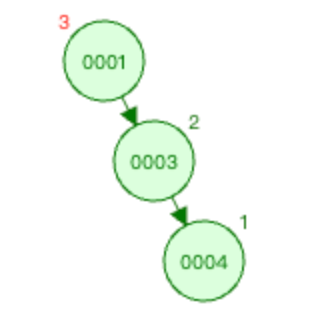
上图中 麻烦节点 为0004(新插入节点),被破坏节点 为0001。
在 被破坏节点 0001节点的 右边 (0001-->0003为右)节点(0003节点)的 右边 (0003-->0004为右)插入新节点0004。
图2:
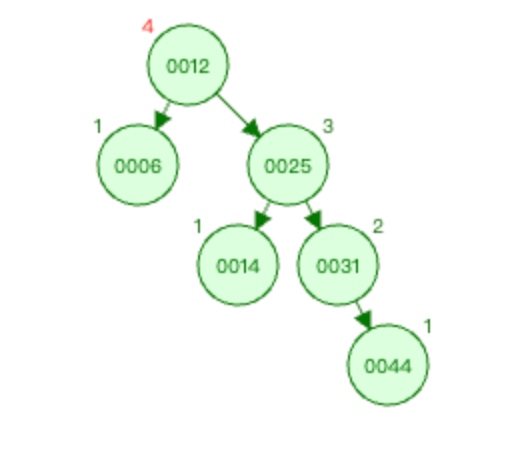
上图中 麻烦节点 为0044(新插入节点),被破坏节点 为0012。
在 被破坏节点 0012节点的 右边 (0012-->0025为右)节点(0025节点)的 右边 (0025-->0031为右)插入新节点0044。
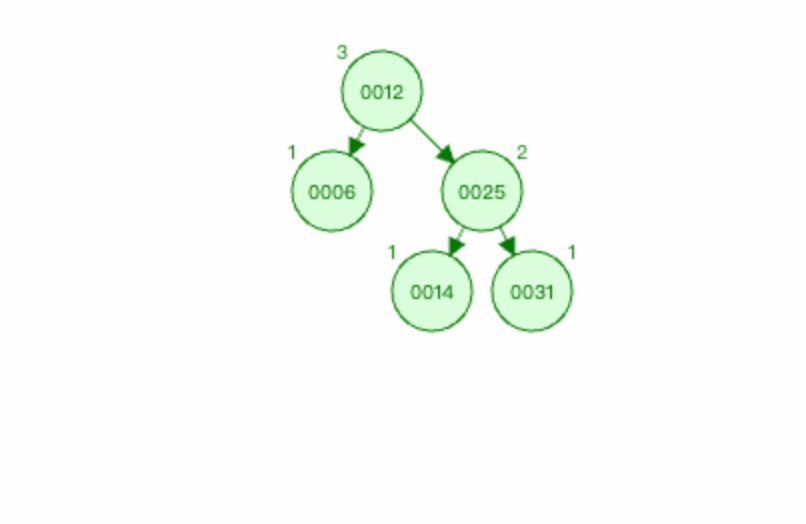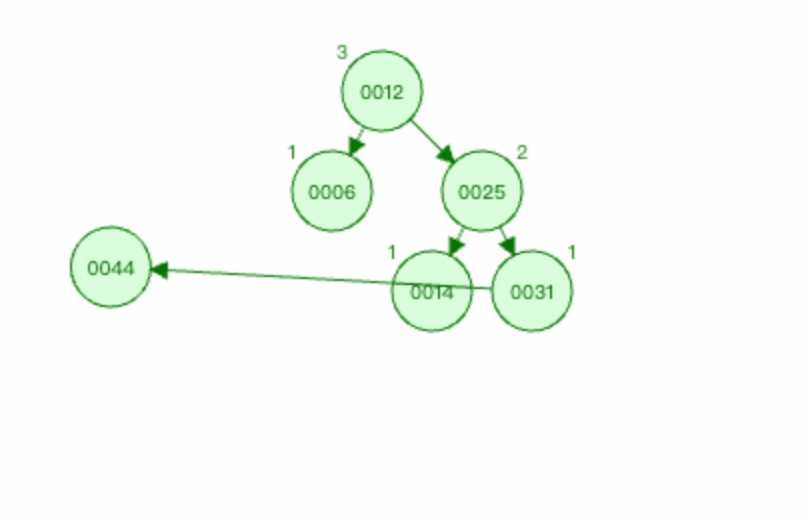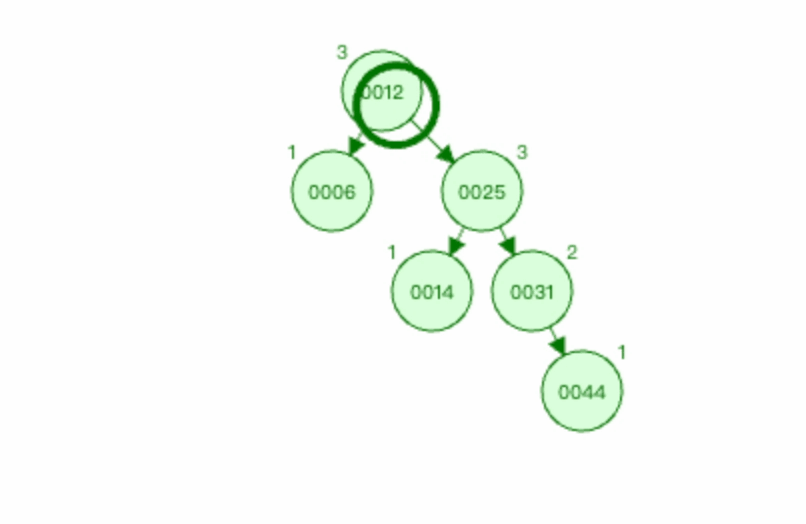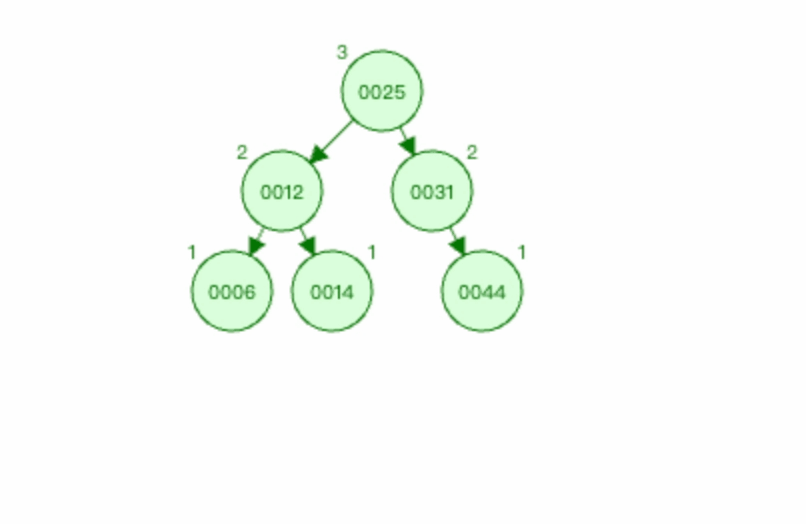
图3:
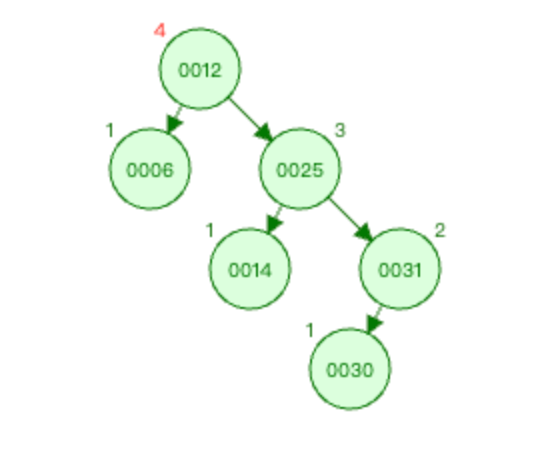
上图中 麻烦节点 为0030(新插入节点),被破坏节点 为0012。
在 被破坏节点 0012节点的 右边 (0012-->0025为右)节点(0025节点)的 右边 (0025-->0031为右)插入新节点0044。
上面三张图所示,在被破坏节点的右边的右边插入新节点,从而导致平衡树失衡了,则称之为RR型。虽然上面图2的0044节点是在0031节点的右边插入,而图3的0030节点是在0031节点的左边插入,但是它们还都算是RR型。因为上文也说过,只会从 被破坏节点 开始往下判断两次,不会理会第三次是往左还是往右。
RR型的解决方案是 左旋 。
3.2.2 什么是左旋?
示意图如下
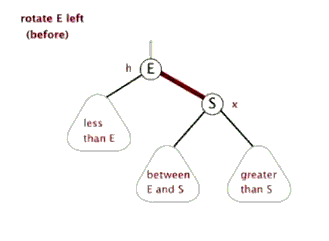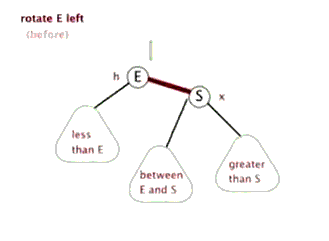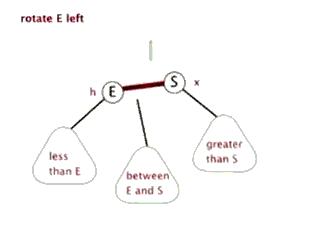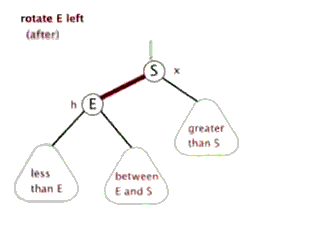
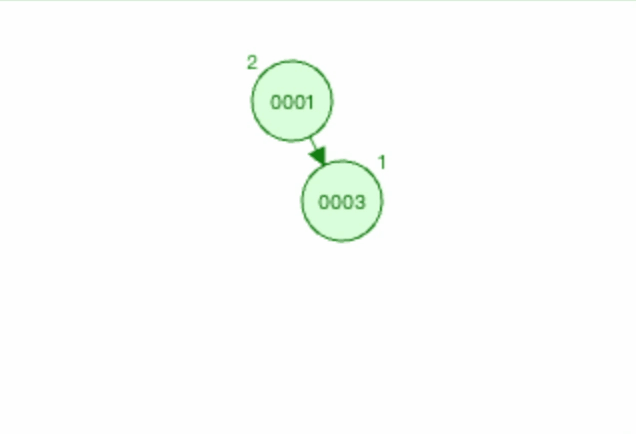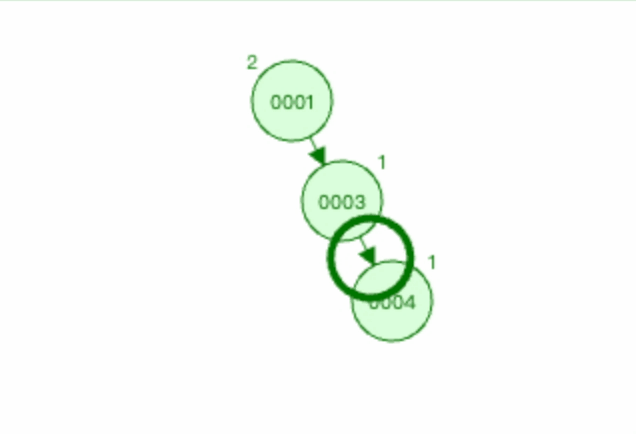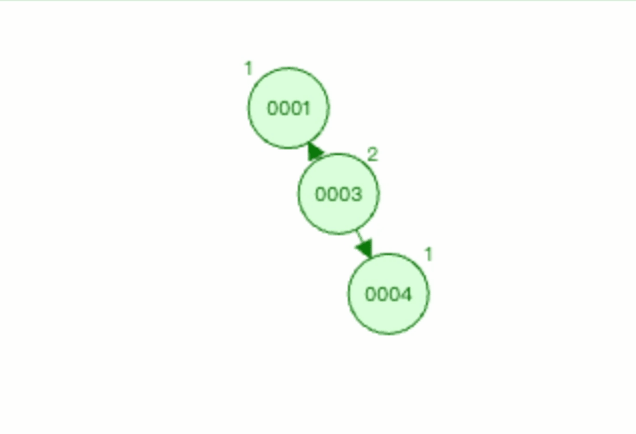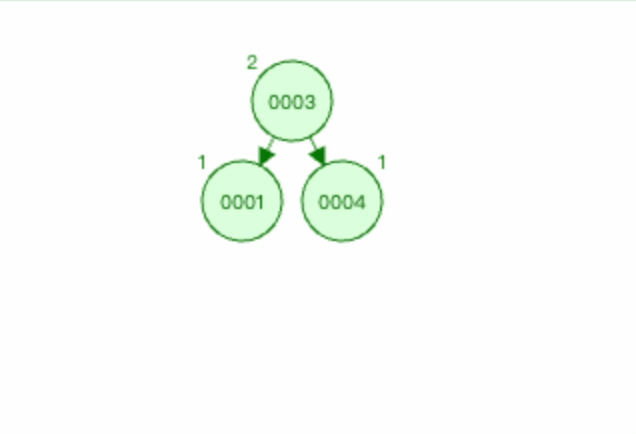
3.2.3 上图1左旋过程如下
以节点0003为基础进行左旋。
3.2.4 上图2左旋过程如下
以节点0025为基点进行左旋。
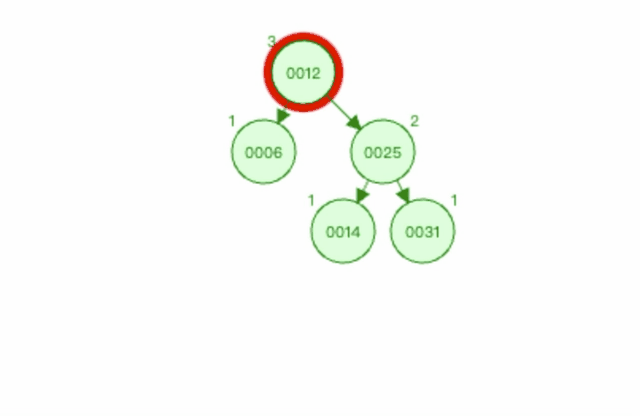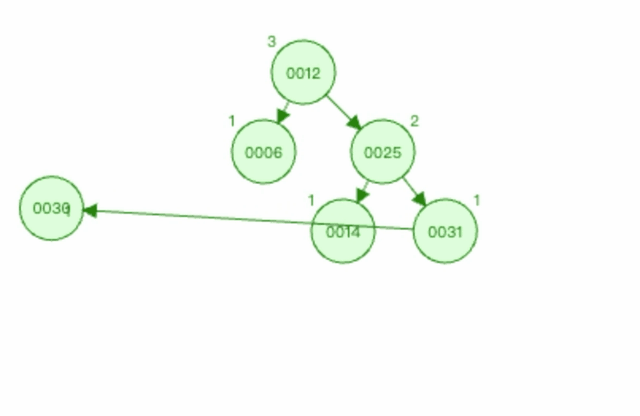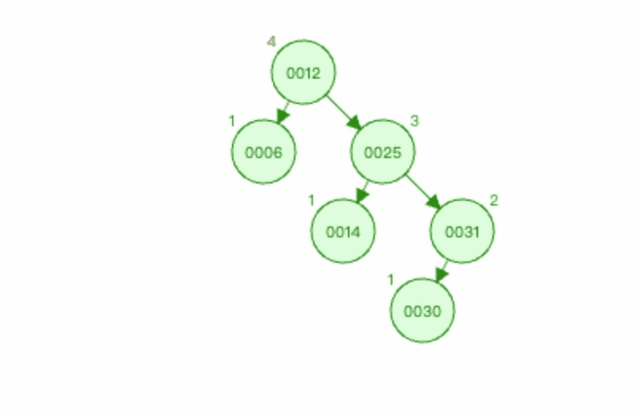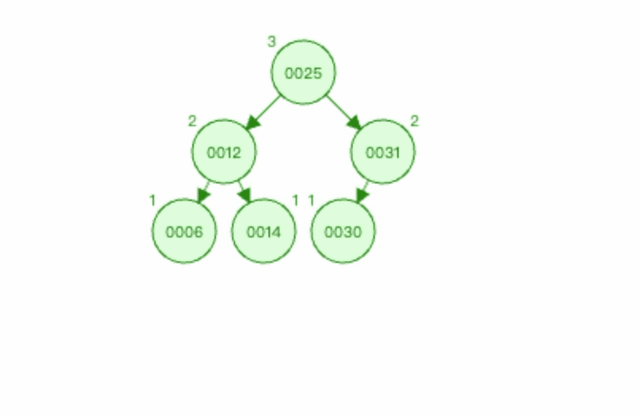
3.2.5 上图3左旋过程如下
以节点0025为基点进行左旋。
3.3 LR型
3.3.1 示例图
图1:
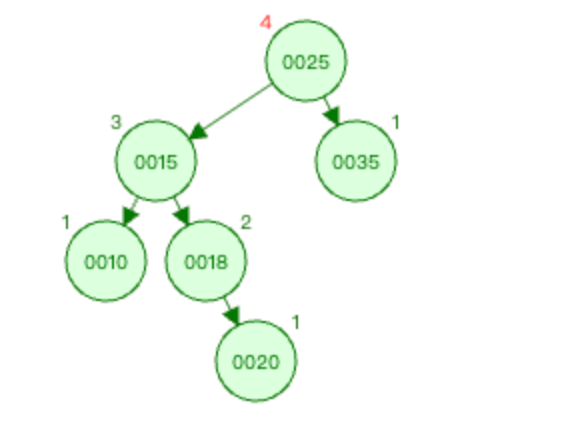
上图1中 麻烦节点 为0020(新插入节点),被破坏节点 为0025。
在 被破坏节点 0025节点的 左边 (0025-->0015为左)节点(0015节点)的 右边 (0015-->0018为右)插入新节点0020。
图2:
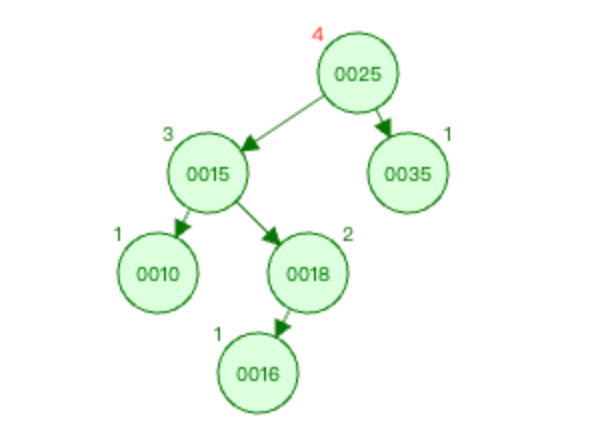
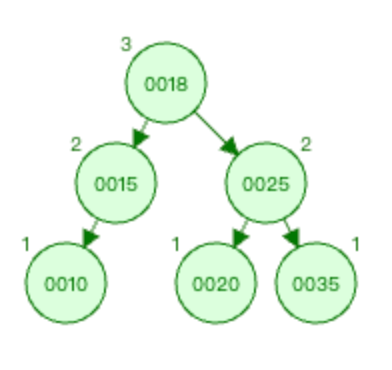
上图1中 麻烦节点 为0016(新插入节点),被破坏节点 为0025。
在 被破坏节点 0025节点的 左边 (0025-->0015为左)节点(0015节点)的 右边 (0015-->0018为右)插入新节点0016。
上面两图所示,在被破坏节点的左边的节点的右边插入新节点,从而导致平衡树失衡了,则称之为LR型。
同样此处也只会从 被破坏节点 开始往下判断两次,不会理会第三次是往左还是往右。
LR型的解决方案为,先根据 被破坏节点 的左子节点为根结点,进行左旋,然后以 被破坏节点 为根结点进行右旋。
3.3.2 上图1平衡调整过程如下
先根据
被破坏节点的节点0025 的左子节点0015为根结点,进行左旋操作。以0015节点为根结点左旋,则是以0018节点为基础进行左旋。具体操作可参考上文中的RR型操作的左旋。
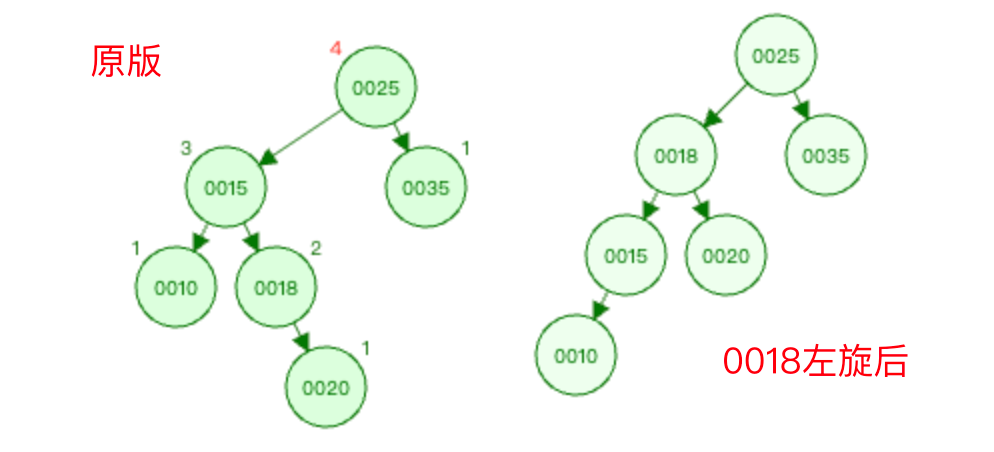
然后以
被破坏节点的节点0025为根结点进行右旋操作。以0025节点为根结点进行右旋,则是以节点0018为基础进行右旋操作。
则 节点0018替换原先的节点0025的位置 ,然后 节点0018的左指针指向节点0015 ,0025-->0018的路径调整为0018-->0025,节点0025变为节点0018的右子树 。
那原先节点0018右指针指向的节点0020就被摘了出来,因为是0020比0018大,是0018原先的右子树,所以得放到0018节点的右边去进行比对,先比对0018右子树节点0025,发现0020<0025,则 0020挂到0025节点的左子树节点 即可。
3.3.3 上图2平衡调整过程如下
先根据
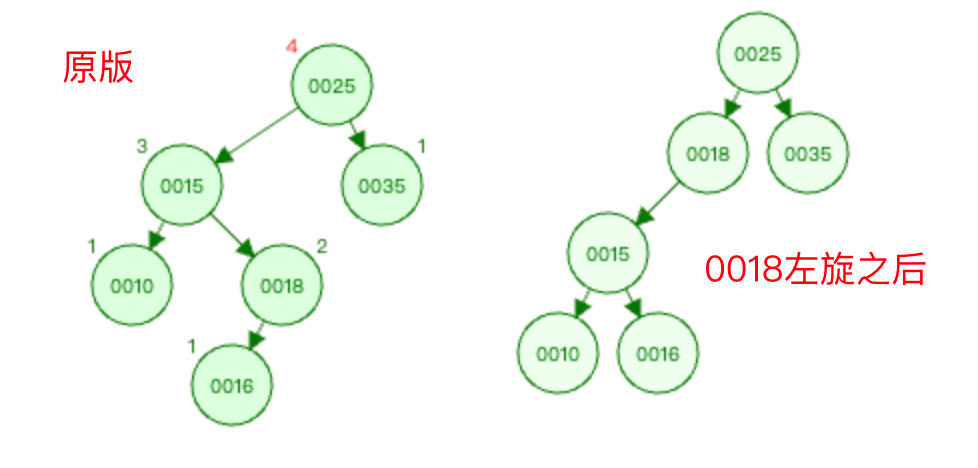
被破坏节点的节点0025的左子节点0015节点为根结点,进行左旋操作。以0015节点为根结点左旋,则是以0018节点为基础进行左旋。
则 节点0018替换原先的节点0015位置 ,然后 节点0018的左指针指向节点0015 ,右指针按理应该是指向节点0016的,但是0016小于0018,如果在0018的右边,则不符合二叉树右子树大于其根节点的定义。
所以将节点0016摘出来,放到节点0018的左边进行比对,然后比对节点0015,发现0016比0015大,则 0016挂到0015节点的右子树 即可。
此时便完成了以0018节点为基础的左旋操作。
然后再以
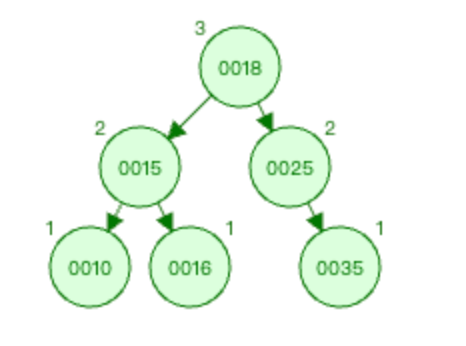
被破坏节点的节点0025为根结点进行右旋操作。以0025节点为根结点进行右旋,则是以节点0018为基础进行右旋操作。
则 节点0018替换原先的节点0025位置,0025-->0018的路径调整为0018-->0025,节点0025变为节点0018的右子树。
此时便完成了整个树的平衡调整操作。
3.4 RL型
3.4.1 示例图

上图中 麻烦节点 为0019(新插入节点),被破坏节点 为0018。
在 被破坏节点 0018节点的 右边 (0018-->0025为右)节点(0025节点)的 左边 (0025-->0020为左)插入新节点0019。
因为在被破坏节点的右边的节点的左边插入新节点插入新节点,导致平衡二叉树失衡的为RL型。
RL型的解决方式和LR型的解决思路是一样的。RL型的解决方案为,先根据 被破坏节点 的右子节点为根结点,进行右旋,然后以 被破坏节点 为根结点进行左旋。
3.4.2 平衡调整过程如下
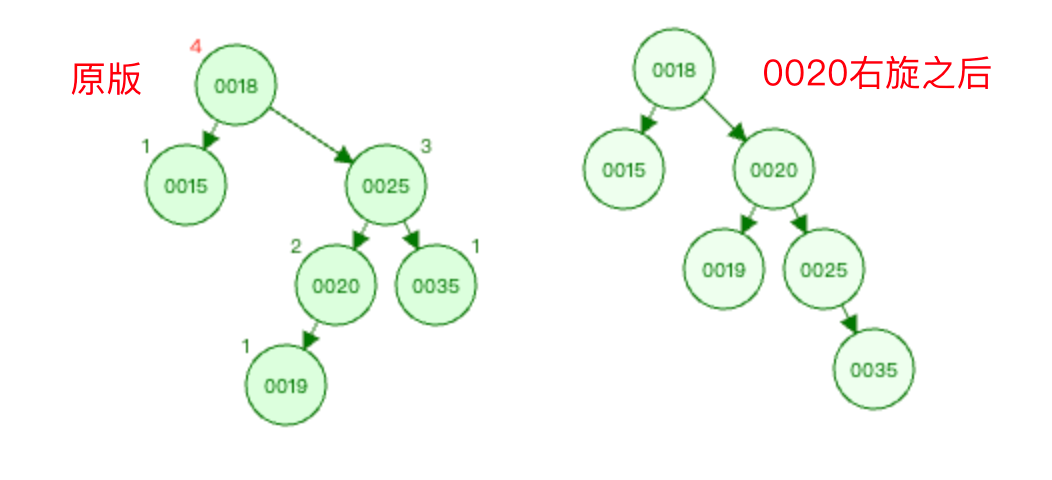
先根据
被破坏节点的节点0018的右子节点0025节点为根结点,进行右旋操作。以0018节点的右子节点为根结点右旋,则是以0020节点为基础进行右旋操作。
然后再以
被破坏节点的节点0018为根结点进行左旋操作。以0018节点为根结点左旋,则是以0020节点为基础进行左旋操作。
则 节点0020替换原先的节点0018位置 ,0018-->0020的路径调整为0020-->0018, 节点0018变为节点0020的左子树节点 ,然后 节点0020的右指针依旧指向节点0025 。
所以就将节点0019给摘了出来,放到节点0020的左边进行比对,然后比对节点0018,发现0019比0018大,则 0019挂到0018节点的右子树 即可。
3.5 总结说明
由上面这些案例可以总结出如下经验:
从
被破坏节点开始往麻烦节点方向判断两次(两个节点之间的路径为一次判断,路径向左即为L,路径向右即为R)即得到破坏平衡性的场景类型。LL型和RR型的处理方式为以
被破坏节点为基础进行其型号相反的方向进行旋转,LL型为右旋,RR型为左旋。LR型和RL型都需要进行两次旋转,第一次旋转方向为型号从左到右的首字母,即LR型的第一次旋转,为以
被破坏节点的左子树节点为根结点,进行左旋操作。RL型的第一次旋转,为以被破坏节点的右子树节点为根结点,进行右旋操作。第二次旋转方向为型号从左到右的结尾字母,即LR型第二次旋转,为以被破坏节点为根节点进行右旋操作。RL型第二次旋转,为以被破坏节点为根结点进行左旋操作。
4 平衡二叉树的节点删除
4.1 LL型

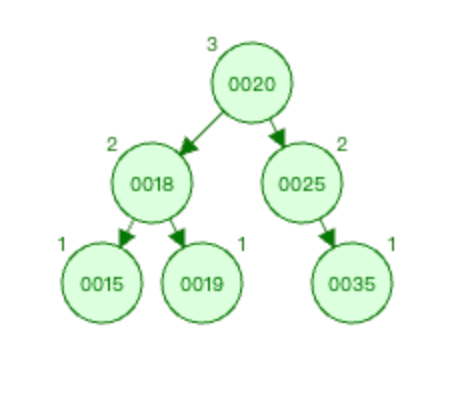
删除节点0025,则会导致节点0020的平衡性被破坏,所以0020节点为 被破坏节点 。
删除节点0025之后,可以看到节点0020的左边深度为3(0020-->0018-->0015),右边深度为1(0020)。所以 平衡因子 为2,其深度差大于1。
删除节点0025之后的情况如下图
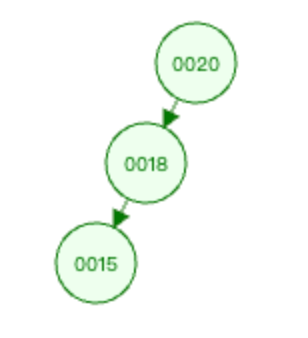
这个图就和0015节点是新插入节点的场景是一样的,可以判断出为LL型的失衡。之后的处理方式也和LL型节点插入一样的,对其进行右旋即可。
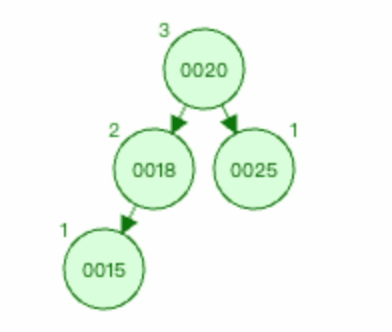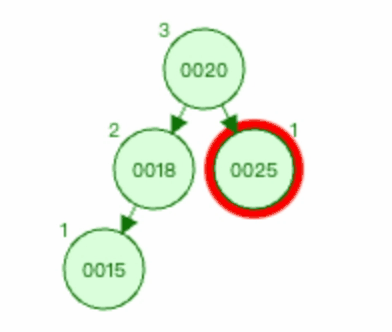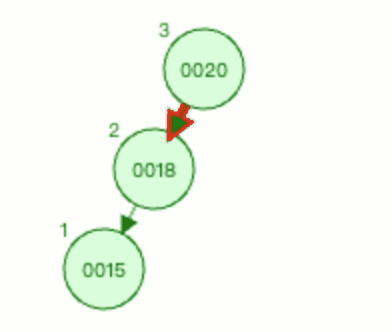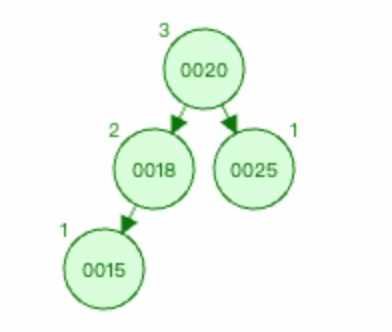
4.2 RR型
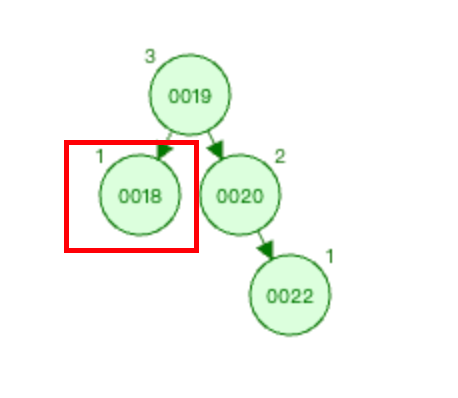
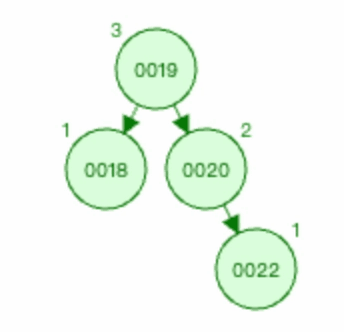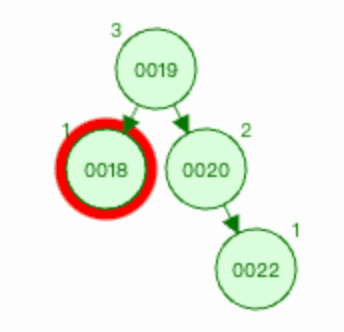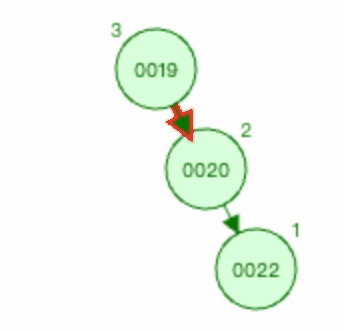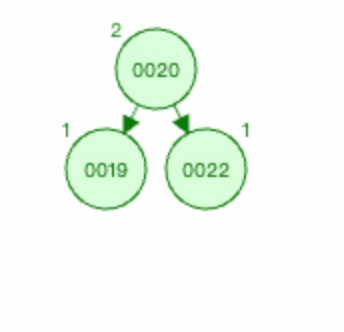
删除节点0018,则会导致节点0019的平衡性被破坏,所以0019节点为 被破坏节点 。
删除节点0018之后,可以看到节点0019的左边深度为1(0019),右边深度为3(0019-->0020-->0022)。所以 平衡因子 为-2,绝对值为2,其深度差大于1。
删除节点0018之后的情况如下图
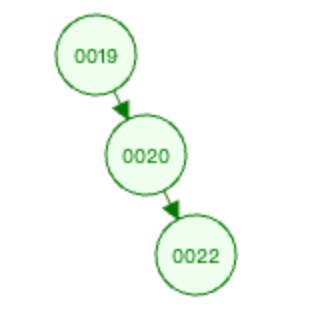
这个图就和0022节点是新插入节点的场景是一样的,可以判断出为RR型的失衡。之后的处理方式也和RR型节点插入一样的,对其进行左旋即可。
4.3 LR型
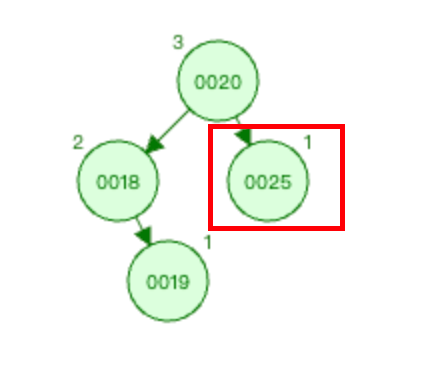
删除节点0025之后,则会导致节点0020的平衡性被破坏,所以0020节点为 被破坏节点 。
删除节点0025之后的情况如下图
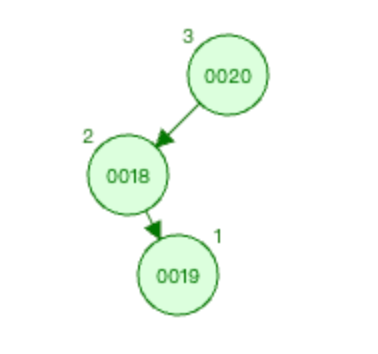
就相当于是0019节点是新插入节点的场景是一样的,可以判断出为LR型的失衡(0020-->0018为左,0018-->0019为右)。之后的处理方式也和LR型节点插入一样的,先根据 被破坏节点 的左子节点为根结点,进行左旋,然后以 被破坏节点 为根结点进行右旋。
先根据
被破坏节点的节点0020的左子节点0018为根结点,进行左旋操作。以0018节点为根结点进行左旋,则是以节点0019为基础进行左旋操作。
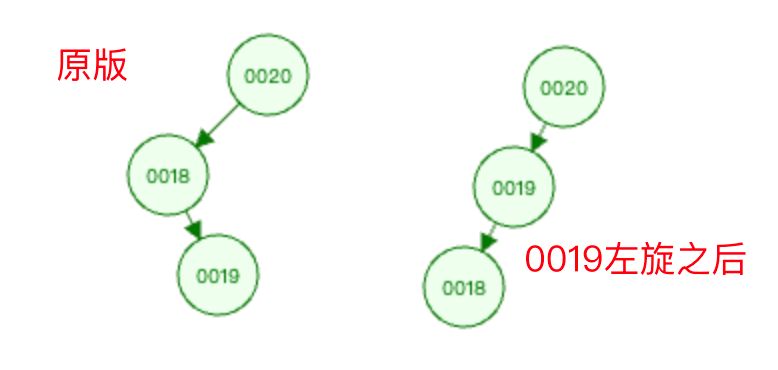
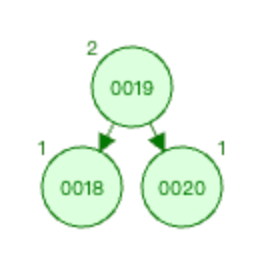
然后以
被破坏节点的节点0020为根结点进行右旋操作。以0020节点为根结点进行右旋,则是以节点0019为基础进行右旋操作。
4.4 RL型

删除节点0019之后,则会导致节点0020的平衡性被破坏,所以0020节点为 被破坏节点 。
删除节点0019之后的情况如下图
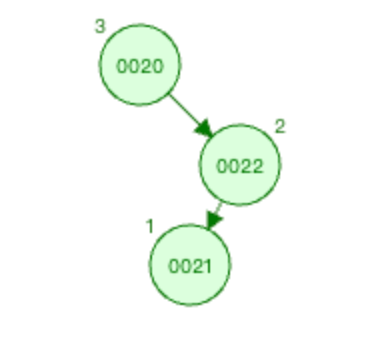
就相当于是0021节点是新插入节点的场景是一样的,可以判断出为RL型的失衡(0020-->0022为右,0022-->0021为左)。之后的处理方式也和RL型节点插入一样的,先根据 被破坏节点 的右子节点为根结点,进行右旋,然后以 被破坏节点 为根结点进行左旋。
先根据
被破坏节点的节点0020的右子节点0022为根结点,进行右旋操作。以0022节点为根结点进行右旋,则是以节点0021为基础进行右旋操作。
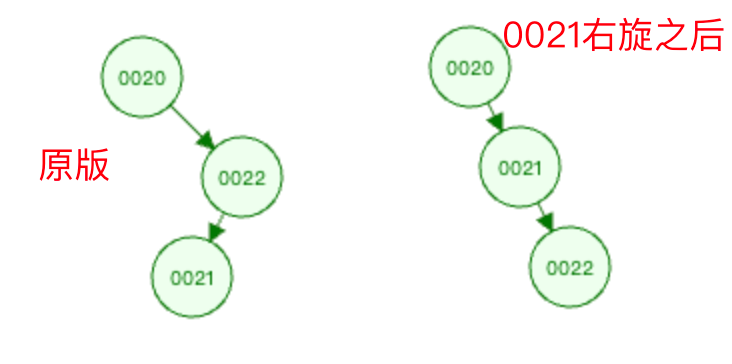
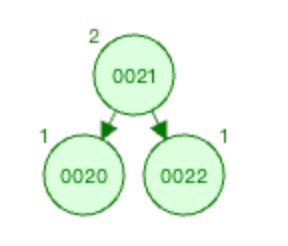
然后以
被破坏节点的节点0020为根结点进行左旋操作。以0020节点为根结点进行左旋,则是以节点0021为基础进行左旋操作。
4.5 总结说明
平衡二叉树的删除节点之后,其平衡调整操作的思想,基本上和插入节点导致平衡二叉树失衡,而进行平衡调整操作是一样的。
